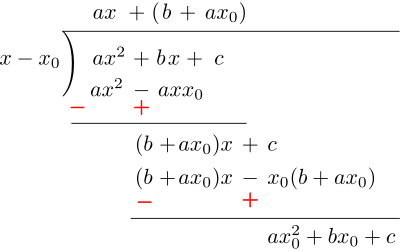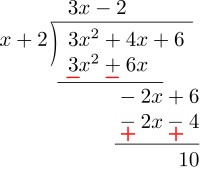Quadratic Expressions
Any expression of the form
\[f(x) = ax^2 + bx + c\]where the constants \(a\,(\neq0)\), \(b\), and \(c\) belong to the set of real numbers \(\mathbb{R}\) while \(x\) is a variable that can take any value from \(\mathbb{R}\), is called a quadratic expression.
For any given value of \(x\), say \(x_0\), the above expression will have a particular value, which can be obtained by replacing \(x\) by \(x_0\) in the formula. We shall denote this value as \(f(x_0)\); i.e.,
\[f(x_0) = a{x_0}^2 + b{x_0} + c\]For example, \(f(x) = 2x^2 - 2x + 1\) is a quadratic expression and \(f(0) = 1\). Similarly, \(f(x) = -x^2\) is a quadratic expression, but \(f(x) = -2x + 3\) is not a quadratic expression.
Roots of a Quadratic Expression
A root or zero of a quadratic expression is that value of the variable \(x\) for which the value of the quadratic expression is zero.
That is, \(x = \alpha\) is a root of \(f(x) = ax^2 + bx + c\) if and only if \(f(\alpha) = a\alpha^2 + b\alpha + c = 0\). Thus, \(x = 1\) is a root of \(f(x) = x^2 - 1\), because \(f(1) = 0\).
Note: It is not necessary that every quadratic expression will have a real root. For example, \(f(x) = x^2 + x + 1\) has no real roots.
Remainder Theorem
Now, let us take an arbitrary value of \(x\), say \(x = x_0\). If we divide \(f(x) = ax^2 + bx + c\) by \((x - x_0)\) using the long division method, we obtain the following result:
The remainder \(ax_0^2 + bx_0 + c\) is simply the value of the expression evaluated at \(x = x_0\), i.e., the remainder is \(f(x_0)\).
Denoting by \(Q(x)\) the expression \(ax + ax_0 + b\), we finally obtain:
\[f(x) = (x - x_0)Q(x) + f(x_0)\]This result simply states that:
When a quadratic expression \(ax^2 + bx + c\) is divided by a linear factor \((x - x_0)\), the remainder is the value of the expression evaluated at \(x = x_0\).
This statement is known as the Remainder Theorem, a fundamental result of algebra.
For instance, when \(3x^2 + 4x + 6\) is divided by \(x+2\), the remainder is:
\[3(-2)^2 + 4(-2) + 6 = 10\]which can also be verified by direct division:
The remainder theorem is valid for any polynomial, not just quadratics. For example, if the polynomial \(P(x) = x^3 + 1\) is divided by \((x+2)\), the remainder is \(P(-2) = -7\), which can be checked:
Factor Theorem
Going back to the quadratic expression \(f(x) = ax^2 + bx + c\), if \(x_0\) is a root of \(f(x)\), then \(f(x_0) = 0\) and the remainder theorem reduces to:
\[f(x) = (x - x_0)Q(x)\]That is:
If \(x = x_0\) is a root of \(f(x)\), then \((x - x_0)\) is a factor of the quadratic expression.
This is known as the Factor Theorem, a special case of the Remainder Theorem.
Graph of a Quadratic Expression
Consider the quadratic expression:
\[f(x) = ax^2 + bx + c\]where the constants \(a\,(\neq0)\), \(b\), and \(c\) are real numbers.
Assigning \(f(x) = y\), we plot points \((x,y)\) in the Cartesian plane. The collection of all such points where \(y = ax^2 + bx + c\) forms the graph of the quadratic expression, which is a parabola.
An example is shown below:
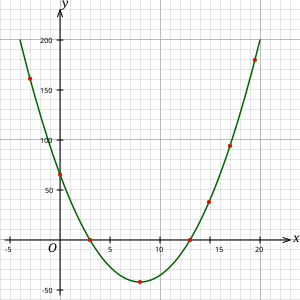Figure 1: The graph of a quadratic expression is a parabola. The graph above is of the expression:
The red dots are some calculated points.*
Further Investigations
Intersection with x-axis
Finding the roots of a quadratic expression means finding values of \(x\) such that \(f(x) = 0\).
As the \(y\)-values correspond to \(f(x)\), when \(f(x) = 0\), the point lies on the \(x\)-axis.
Thus, finding roots is equivalent to finding the intersection points of the parabola with the \(x\)-axis.
We can solve \(f(x) = 0\) using the Sridharacharya formula. Let the roots be \(\alpha\) and \(\beta\). Then:
\[f(x) = a(x - \alpha)(x - \beta)\]This factorization follows from Vieta’s Relations as well:
\[\begin{aligned} f(x) &= a(x - \alpha)(x - \beta) \\ &= a(x^2 - (\alpha + \beta)x + \alpha\beta) \\ &= ax^2 + bx + c \end{aligned}\]Depending on the discriminant \(D = b^2 - 4ac\), three cases arise:
‣ Case I: \(b^2 - 4ac > 0\)
In this case, both \(\alpha\) and \(\beta\) are real. Suppose \(\alpha > \beta\).
When \(a > 0\):
- \(f(x) > 0\) for \(x < \beta\) and \(x > \alpha\).
- \(f(x) < 0\) between \(\beta\) and \(\alpha\).
- The graph cuts the \(x\)-axis at two points.
- The parabola opens upward.
When \(a < 0\):
- \(f(x) < 0\) for \(x < \beta\) and \(x > \alpha\).
- \(f(x) > 0\) between \(\beta\) and \(\alpha\).
- The graph cuts the \(x\)-axis at two points.
- The parabola opens downward.
Figure 2: Possible shapes when the discriminant is positive (\(b^2-4ac>0\)).
‣ Case II: \(b^2 - 4ac = 0\)
Here, there is a single real root \(\alpha\).
When \(a > 0\):
- \(f(x) > 0\) for all \(x \neq \alpha\).
- The graph touches the \(x\)-axis at one point.
- The parabola opens upward.
When \(a < 0\):
- \(f(x) < 0\) for all \(x \neq \alpha\).
- The graph touches the \(x\)-axis at one point.
- The parabola opens downward.
Figure 3: Possible shapes when the discriminant is zero (\(b^2-4ac=0\)).
‣ Case III: \(b^2 - 4ac < 0\)
Here, the roots are complex and the graph does not intersect the \(x\)-axis.
When \(a > 0\):
- \(f(x) > 0\) for all real \(x\).
- The parabola opens upward.
When \(a < 0\):
- \(f(x) < 0\) for all real \(x\).
- The parabola opens downward.
Figure 4: Possible shapes when the discriminant is negative (\(b^2-4ac<0\)).
• Summary
Below are all six possible shapes of the quadratic expression \(f(x) = ax^2 + bx + c\).
Figure 5: Summary of all possible shapes.
Maximum or Minimum Value
To find the extremum of \(f(x) = ax^2 + bx + c\):
Complete the square:
\[f(x) = a \left(x + \frac{b}{2a}\right)^2 - \frac{D}{4a}\]where \(D = b^2-4ac\).
- If \(a>0\): Minimum value \(= -\dfrac{D}{4a}\) at \(x = -\dfrac{b}{2a}\).
- If \(a<0\): Maximum value \(= -\dfrac{D}{4a}\) at \(x = -\dfrac{b}{2a}\).
If the quadratic has real and distinct roots, the extremum occurs exactly midway between the roots.